Advanced Tutorials

diffpy.morph has some more functionalities not showcased in the quickstart tutorial. Tutorials for these are included below. The files required for these tutorials can be downloaded here.

For a full list of options offered by diffpy.morph, please run diffpy.morph --help on the command line.

Performing Multiple Morphs

It may be useful to morph a PDF against multiple targets: for example, you may want to morph a PDF against multiple PDFs measured at various temperatures to determine whether a phase change has occurred. diffpy.morph currently allows users to morph a PDF against all files in a selected directory and plot resulting \(R_w\) values from each morph.

  1. Within the additionalData directory, cd into the morphsequence directory. Inside, you will find multiple PDFs of \(SrFe_2As_2\) measured at various temperatures. These PDFs are from “Atomic Pair Distribution Function Analysis: A primer”.

  2. Let us start by getting the \(R_w\) of SrFe2As2_150K.gr compared to all other files in the directory. Run

    diffpy.morph SrFe2As2_150K.gr . --multiple-targets

    The multiple tag indicates we are comparing PDF file (first input) against all PDFs in a directory (second input). Our choice of file was SeFe2As2_150K.gr and directory was the cwd, which should be morphsequence.

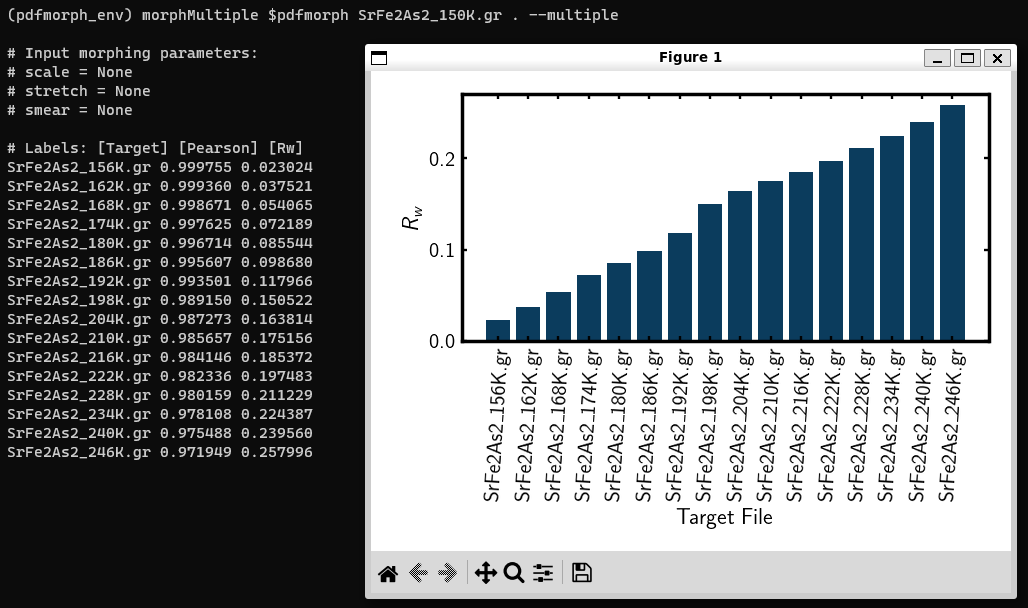
_images/ex_tutorial_bar.png

Bar chart of \(R_W\) values for each target file. Target files are listed in ASCII sort order.

  1. After running this, we get chart of \(R_w\) values for each target file. However, this chart can be a bit confusing to interpret. To get a more understandable plot, run

    diffpy.morph SrFe2As2_150K.gr . --multiple-targets --sort-by=temperature

    This plots the \(R_w\) against the temperature parameter value provided at the top of each file. Parameters are entries of the form <parameter_name> = <parameter_value> and are located above the r versus gr table in each PDF file.

    # SrFe2As2_150K.gr
[PDF Parameters]
temperature = 150
wavelength = 0.1
...
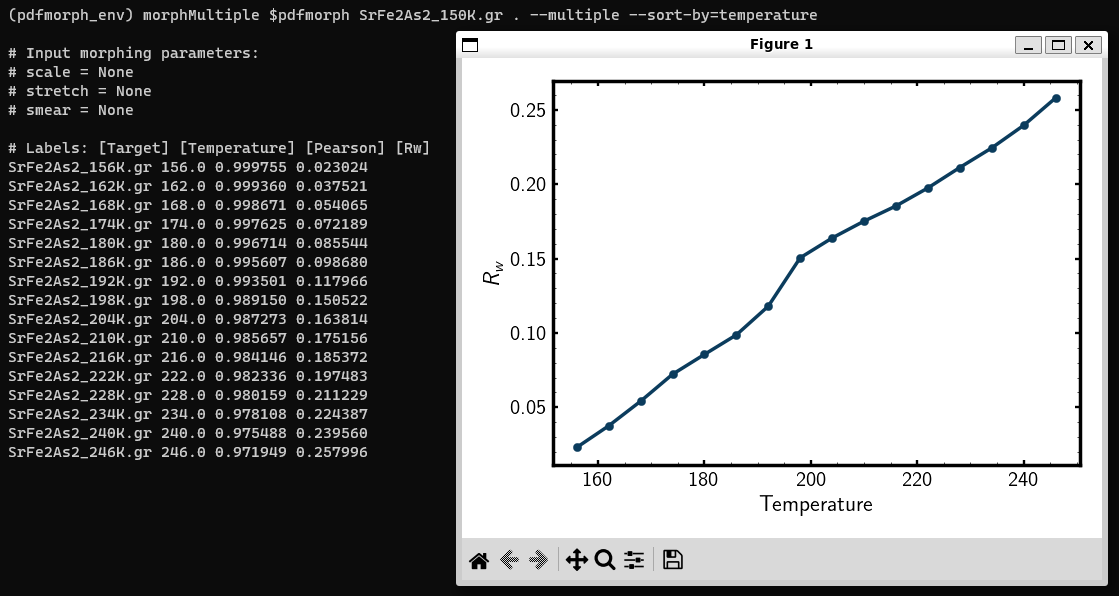
_images/ex_tutorial_temp.png

The \(R_W\) plotted against the temperature the target PDF was measured at.

  1. Between 192K and 198K, the Rw has a sharp increase, indicating that we may have a phase change. To confirm, let us now apply morphs onto `` SrFe2As2_150K.gr`` with all other files in morphsequence as targets

    diffpy.morph --scale=1 --stretch=0 SrFe2As2_150K.gr . --multiple-targets --sort-by=temperature

    Note that we are not applying a smear since it takes a long time to apply and does not significantly change the Rw values in this example.

  2. We should now see a sharper increase in \(R_w\) between 192K and 198K.

  3. Go back to the terminal to see optimized morphing parameters from each morph.

  4. On the morph with SrFe2As2_192K.gr as target, scale = 0.972085 and stretch = 0.000508 and with SrFe2As2_198K.gr as target, scale = 0.970276 and stretch = 0.000510. These are very similar, meaning that thermal lattice expansion (accounted for by stretch) is not occurring. This, coupled with the fact that the Rw significantly increases suggests a phase change in this temperature regime. (In fact, \(SrFe_2As_2\) does transition from orthorhombic at lower temperature to tetragonal at higher temperature!). More sophisticated analysis can be done with PDFgui.

  5. Finally, let us save all the morphed PDFs into a directory named saved-morphs.

    diffpy.morph SrFe2As2_150K.gr . --scale=1 --stretch=0 --multiple-targets \
--sort-by=temperature --plot-parameter=stretch \
--save=saved-morphs

    Entering the directory with cd and viewing its contents with ls, we see a file named morph-reference-table.txt with data about the input morph parameters and re- fined output parameters and a directory named morphs containing all the morphed PDFs. See the --save-names-file option to see how you can set the names for these saved morphs!

Polynomial Squeeze Morph

Another advanced feature in diffpy.morph is the MorphSqueeze morph, which applies a user-defined polynomial to squeeze the morph function along the x-axis. This provides a flexible way to correct for higher-order distortions that simple shift or stretch morphs cannot fully address. Such distortions can arise from geometric artifacts in X-ray detector modules, including tilts, curved detection planes, or angle-dependent offsets, as well as from intrinsic structural effects in the sample.

A first-order squeeze polynomial recovers the behavior of simple shift or stretch, while higher-order terms enable non-linear corrections. The squeeze transformation is defined as:

\[\Delta r(r) = a_0 + a_1 r + a_2 r^2 + \dots + a_n r^n\]

where \(a_0, a_1, ..., a_n\) are the polynomial coefficients defined by the user.

In this example, we show how to apply a squeeze morph in combination with a scale morph to match a morph function to its target. The required files can be found in additionalData/morphsqueeze/.

  1. cd into the morphsqueeze directory:

    cd additionalData/morphsqueeze

    Here you will find:

    • squeeze_morph.cgr — the morph function with a small built-in polynomial distortion.

    • squeeze_target.cgr — the target function.

  2. Suppose we know that the morph needs a quadratic and cubic squeeze, plus a scale factor to best match the target. As an initial guess, we can use:

    • squeeze = 0,-0.001,-0.0001,0.0001 (for a polynomial: \(a_0 + a_1 x + a_2 x^2 + a_3 x^3\))

    • scale = 1.1

    The squeeze polynomial is provided as a comma-separated list (no spaces):

    diffpy.morph --scale=1.1 --squeeze=0,-0.001,-0.0001,0.0001 -a squeeze_morph.cgr squeeze_target.cgr

  3. diffpy.morph will apply the polynomial squeeze and scale, display the initial and refined coefficients, and show the final difference Rw.

    To refine the squeeze polynomial and scale automatically, remove the -a tag if you used it. For example:

    diffpy.morph --scale=1.1 --squeeze=0,-0.001,-0.0001,0.0001 squeeze_morph.cgr squeeze_target.cgr

  4. Check the output for the final squeeze polynomial coefficients and scale. They should match the true values used to generate the test data:

    • squeeze = 0, 0.01, 0.0001, 0.001

    • scale = 0.5

    diffpy.morph refines the coefficients to minimize the residual between the squeezed, scaled morph function and the target.

Warning

Extrapolation risk: A polynomial squeeze can shift morph data outside the target’s r-range, so parts of the output may be extrapolated. This is generally fine if the polynomial coefficients are small and the distortion is therefore small. If your coefficients are large, check the plots carefully — strong extrapolation can produce unrealistic features at the edges. If needed, adjust the coefficients to keep the morph physically meaningful.

Experiment with your own squeeze polynomials to fine-tune your morphs — even small higher-order corrections can make a big difference!

Nanoparticle Shape Effects

A nanoparticle’s finite size and shape can affect the shape of its PDF. We can use diffpy.morph to morph a bulk material PDF to simulate these shape effects. Currently, the supported nanoparticle shapes include: spheres and spheroids.

  • Within the additionalData directory, cd into the morphShape subdirectory. Inside, you will find a sample Ni bulk material PDF Ni_bulk.gr. This PDF is from `”Atomic Pair Distribution Function Analysis: A primer” <https://global.oup.com/academic/product/

    atomic-pair-distribution-function-analysis-9780198885801>`_.

    There are also multiple .cgr files with calculated Ni nanoparticle PDFs.

  • Let us apply various shape effect morphs on the bulk material to reproduce these calculated PDFs.

    • Spherical Shape

      1. The Ni_nano_sphere.cgr file contains a generated spherical nanoparticle with unknown radius. First, let us plot Ni_blk.gr against Ni_nano_sphere.cgr

        diffpy.morph Ni_bulk.gr Ni_nano_sphere.cgr

        Despite the two being the same material, the Rw is quite large. To reduce the Rw, we will apply spherical shape effects onto the PDF. However, in order to do so, we first need the radius of the spherical nanoparticle.

      2. To get the radius, we can first observe a plot of Ni_nano_sphere.cgr

        diffpy.morph Ni_nano_sphere.cgr Ni_nano_sphere.cgr

        Nanoparticles tend to have broader peaks at r-values larger than the particle size, corresponding to the much weaker correlations between molecules. On our plot, beyond r=22.5, peaks are too broad to be visible, indicating our particle size to be about 22.4. The approximate radius of a sphere would be half of that, or 11.2.

      3. Now, we are ready to perform a morph applying spherical effects. To do so, we use the --radius parameter

        diffpy.morph Ni_bulk.gr Ni_nano_sphere.cgr --radius=11.2 -a --rmax=30

      4. We can see that the \(Rw\) value has significantly decreased from before. Run without the -a tag to refine

        diffpy.morph Ni_bulk.gr Ni_nano_sphere.cgr --radius=11.2 --rmax=30

      5. After refining, we see the actual radius of the nanoparticle was closer to 12.

    • Spheroidal Shape

      1. The Ni_nano_spheroid.cgr file contains a calculated spheroidal Ni nanoparticle. Again, we can begin by plotting the bulk material against our nanoparticle

        diffpy.morph Ni_bulk.gr Ni_nano_spheroid.cgr

      2. Inside the Ni_nano_spheroid.cgr file, we are given that the equatorial radius is 12 and polar radius is 6. This is enough information to define our spheroid. To apply spheroid shape effects onto our bulk, run

        diffpy.morph Ni_bulk.gr Ni_nano_spheroid.cgr --radius=12 --pradius=6 -a --rmax=30

        Note that the equatorial radius corresponds to the --radius parameter and polar radius to --pradius.

      3. Remove the -a tag to refine.

There is also support for morphing from a nanoparticle to a bulk. When applying the inverse morphs, it is recommended to set --rmax=psize where psize is the longest diameter of the nanoparticle.